时域方法对任意周期信号频率的测量
一、 综述
在数据采集的环境下，信号的频率测量是基本且重要的问题。只有测得被测信号的频率后，才有可能对其实现整周期采样，从而为接下来的数字信号处理创造有利条件。
频率测量，也就是周期测量，目前主要有时域、频域、计数器和频率跟踪等几种方法。本文中使用的方法就是时域测量方法。
本文中的方法是通过测量信号的自相关函数的周期来确定信号的周期，本方法的特点是对信号中的噪声有很强的抑制作用，对波形和谐波的限制都比较低，但是在基本没有噪声的情况，却把自相关的噪声引入到系统中，造成结果不甚理想。
二、 时域测频率原理及算法
一般来说，常见的测量数据大都是用时域的方式表达的，它们反映在直角坐标系中，常用横轴表示时间变量，以纵轴表示随时间变化的物理量。频率测量，也就是测量周期，最基本的方法就是计数。常见的几种时域方法有多周期的平均计数方法、插值法和三点法。时域方法的主要优点是直接、相对简单且较容易估算误差。
下面是几种基本方法的算法介绍：
1．多周期的平均计数方法
在数据采集的环境下，利用计数方法测量信号的频率虽然不太好用，但是可以尝试对它进行改进。多周期的平均计数方法就是其一，对多个周期的采样信号进行计数，然后以其平均值作为频率测量值。
假定采样频率为
如果满足采样频率是被测信号频率的10倍，且采样样本数超过10个周期，则其频率测量的误差可以控制在
2．线性插值法
有时由于相邻两点离零点都有一定距离的时候，计数法的误差是比较大的。不过，这时可以采用插值的方法来减少误差。例如用线性插值法来计算出两点间的过零点位置，还可以使用牛顿插值法和拉格朗日插值法。
插值法对波形有一定的要求，即其必须便于插值运算，例如正弦波形。还要注意，在不同相位出插值的误差也会有所不同。该算法最主要的优点就是简单。
3．三点法
三点法是一种建立在三角函数变换基础上的数据拟合方法。假设被测函数是正弦函数，在等间隔采样的前提下，可以利用相邻3个数据样本，导出求解信号频率的线性方程，进而拟合出方程系数，最终求出频率。
其原理如下：
设信号为
使用三角变换可得：
令
三点法的主要问题是，它要求信号只能是正弦波。
三、 程序的算法说明
用自相关法来测量信号的频率，只是在测量信号的频率时，引入了自相关函数，通过测量自相关函数的周期性来体现信号的周期，进而得到频率。现介绍一下自相关函数的定义和性质。
自相关函数的定义：信号
自相关函数的一个性质就是周期信号的自相关函数还是周期的，并且周期不变。
离散信号的自相关函数的定义式变为：
如果信号
如果信号
式中，
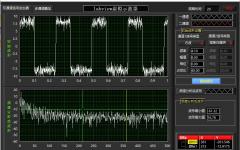
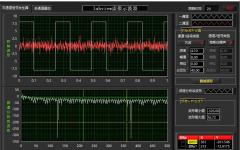
可见信号的自相关函数和原信号具有相同的周期，只是原周期函数的自相关函数叠加了一个噪声的相关函数
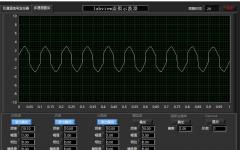
下图上图为叠加了噪声的正弦周期信号
本算法就是基于自相关函数同原信号的同频率这个特性出发产生的。
算法流程图如下：
信号源 低通滤波 自相关处理 截取中间段 数据显示 平均计数法 直接法测量 平均计数法 测量数据一 三点法测量 附件包括开题报告、论文、源程序1本选题的意义及国内外发展状况1.1研究目的和意义 随着工业自动化程度不断发展，对位移测量的精准度、效率以及.. 摘 要:探讨在MATLAB中使用FIS编辑器与Simulink相结合的方法构造模糊推理结构，并通过MATLAB Script Node实现LabVIEW与MATLAB的混合编程，设计出具有模糊自整.. 摘要：针对现代工业过程控制中实时通讯要求和现场总线存在的缺点，用现在流行的开放式标准接口技术OPC规范，设计了一种基于LabV IEW的PC与PCC实时数据通讯方.. 注册时间：2024-12-21 15:45:59 注册时间：2024-12-20 09:42:58 注册时间：2024-12-05 16:34:39 注册时间：2024-11-14 08:49:44 注册时间：2024-11-11 13:46:27
