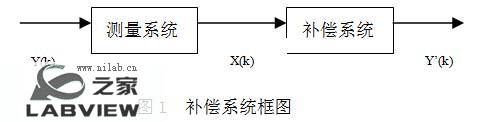
纳秒脉冲信号测量中,在相当宽的频带内实现不失真传输并不容易,测量所得到的往往是畸变的信号。因此,如何恢复真实信号成为人们所关心的问题。随着时域测量技术和数字信号处理技术的发展,用数字手段对测量系统真实输入进行复原为解决这一问题提供了途径。对于测量系统来说,我们希望其输入和输出相同或成线性关系。当测量系统不满足这一要求时,就要尽量设法通过某种算法来恢复真实的输入。这里可以将该算法视为一个补偿系统。如图1所示,补偿系统与测量系统级联,待校正信号X(k)为其输入,Y’(k)为补偿信号。虚拟仪器是二十一世纪的仪器[1],据专家预测,本世纪初我国将有50%的仪器为虚拟仪器[2]。大力发展虚拟仪器对我国现代化建设具有重要意义。本文利用虚拟仪器软件Labview调用MatlabScript节点实现补偿系统的设计。
曾有学者[3]利用反卷积的方法进行波形重建。把传递函数视为h(t),方波响应为g(t),方波输入为1(t),根据Y(jω)=H(jω)X(jω)和G(jω)=H(jω)1(jω)得到:
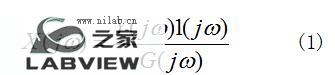
但是由于纳秒脉冲测量中上升时间很短,理想的方波输入和方波响应很难获得,一定程度上限制了这种方法的使用。有学者对波形预测进行过研究[4]。清华大学等离子体实验室、中国工程物理研究院、国防科技大学都曾通过对测量系统进行建模来研究测量系统[5]。国外也有研究人员对脉冲信号重建进行过探讨[6],但是也需要事先获得理想脉冲响应或理想方波响应。
1、补偿原理
1.1 数字滤波器模型补偿
记所设计的数字滤波器离散传递函数为H(z),设其模型形式如下:
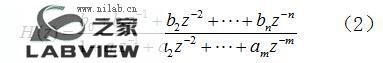
数字滤波器补偿方法的核心就是要确定a1, a2,…am, b0,b1,…bn这m+n+1个参数。上式传递函数所对应的时域输入输出关系为
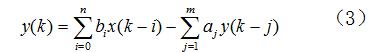
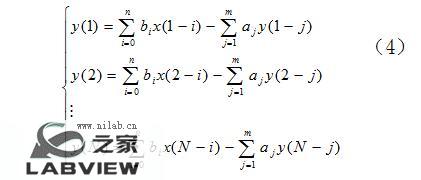
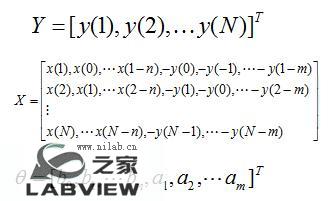
则有如下矩阵方程
θ即为待求参数。而离散传递函数模型参数求取等价于求满足式(5)的解θ。由于观测数据的长度N(也就是方程的个数)远大于未知数的个数(m+n+1),式(5)为矛盾方程组,其解θ可采用最小二乘法求得。
1.2 差分方程模型补偿
假设补偿系统对应的差分方程为:
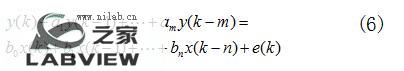
其中a1,…,am,b0,…,bn也是m+n+1个需要辨识的参数,e(k)为噪声干扰。式(6)可以变化为如下形式:
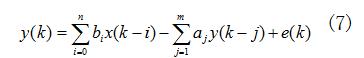
X和θ所代表的矩阵和数字滤波器模型补偿时一致。此时若记
则有如下矩阵方程

根据输入输出数据,利用最优化理论,求出使得H达到极小值的θ值,那么a1,…,am,b0,…,bn这m+n+1个参数也就求得了。从式(6)我们可以看出,利用测量系统的畸变输出x(k),我们只需要赋给y(k)一个初值,利用迭代的方法就可以求得输出y(k),这就实现了对测量系统输出信号的补偿。
2、实验补偿分析
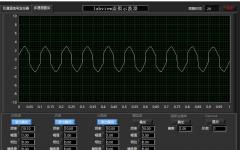
下面通过脉冲发生器产生一上升沿大约为1.6ns、幅值为2.5V的纳秒阶跃波加载到自制的单级电阻分压器进行测量,为了保证信号能够以最大功率传送,阻抗应该匹配[8]。标准纳秒波形数据如表1所示,测量信号数据如表2所示。
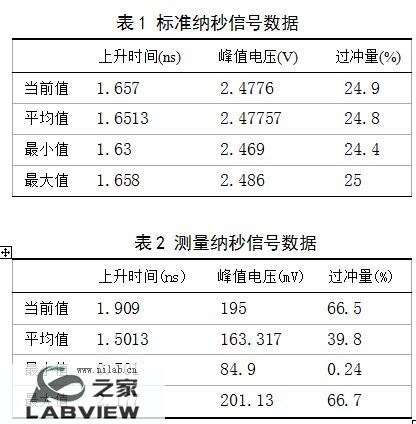
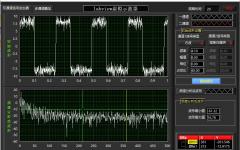
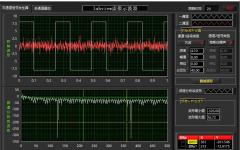
得到两路采集信号以后,输入到所调用的Matlab Script Node中进行处理。Labview使用ActiveX技术来实现Matlab脚本节点,因此Matlab脚本节点只能用于Windows平台上[9]。Matlab Script Node中为补偿程序。运行数字滤波器补偿程序后得到的补偿信号如图2、图3所示。
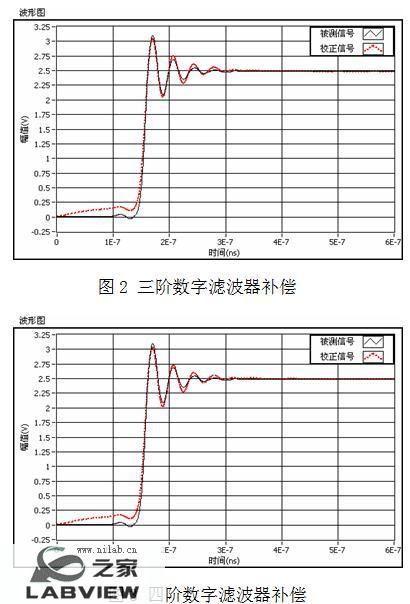
而由此得到的数字滤波器的分子分母系数如表3所示。
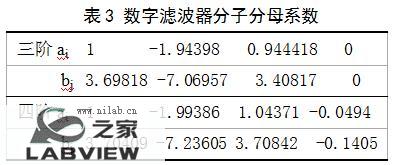
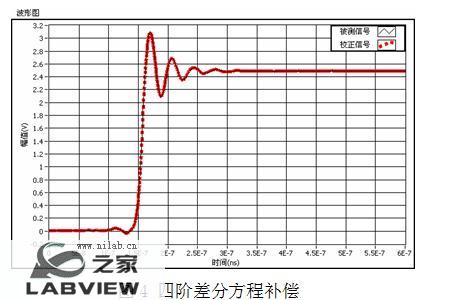
所得差分方程的系数如图5所示。

对应的差分方程为:
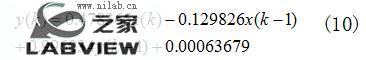
也即补偿系统如果满足式(10),就可以对畸变测量信号进行补偿校正。
由以上两种补偿方法的补偿效果来看,数字滤波器补偿信号基本能跟随被测信号。而差分方程模型补偿信号则更胜一筹。
3、结论
通过实验分析可知,差分方程模型补偿方法和数字滤波器补偿方法都可以对畸变信号进行补偿。但是,差分方程模型补偿可以更好地还原被测信号。因为补偿系统是由软件来实现的,所以这两种方法的实现降低了实际测量探头的苛刻度,又能节约整个测量系统的成本,所以有广泛的适用性。
参考文献
[1] Ai,X.,Yang,Y.,Zhou,X.Virtual Instrument Technology And Its Application to Power System.Dianli Xitong Zidonghua/Automation of Electric Power Systems,2001,25 (15):54-57
[2]薛得风,基于图形化编程语言LabVIEW的一种虚拟仪器的实现,自动化与仪器仪表,2003.5
[3]徐玮,管喜康. 用FFT法重建冲击电压测量系统的输入波形[J]. 高电压技术 1986,(1):43-47.
[4]韩英杰,孙广生,严萍,王珏,张适昌.纳秒脉冲电压的波形重建[J].强激光于粒子束2004,16(4):514-516.
[5]韩英杰.纳秒脉冲信号的测量与波形重建[D].北京:中国科学院电工研究所,2004